Notions et connaissances travaillées :
- Élaborer une explication à un phénomène
- Réaliser que la corrélation n’implique pas forcément une relation de cause à effet
- Pratiquer, avec l’aide du professeur, quelques moments d’une démarche d’investigation
- Utiliser les outils mathématiques adaptés
- Prélever et organiser les informations nécessaires à la résolution de problèmes à partir de supports variés : textes, tableaux, diagrammes, graphiques, dessins, schémas, etc.
Disciplines : Sciences et technologie, Mathématiques
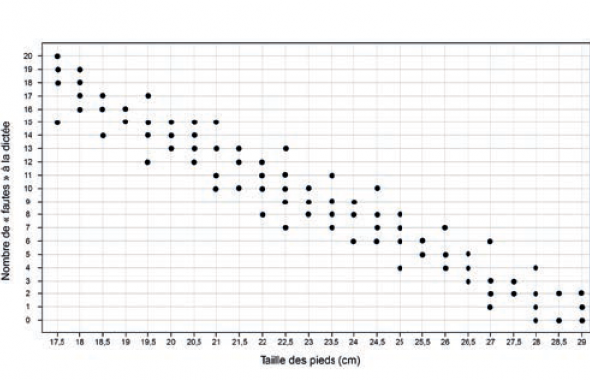
Activité : Pieds et dictée
Déroulé : Les élèves lisent un graphique qui montre l’existence d’une relation particulière entre deux variables: une corrélation (phase 1). Ils collectent et analysent d’autres données au sein de la classe (phase 2), puis commentent ce type de relations avec l’enseignant. Ils développent une réflexion quant aux relations de corrélation et de causes à effets (phase 3). Enfin, ils transposent ces considérations à d’autres situations de sciences et à la vie quotidienne (phase 4).
Message à emporter : Lorsqu’on constate que deux faits sont liés, il faut être capable de distinguer s’il existe entre eux une relation de cause à effet, ou un autre type de relation.
Activité : Une illusion de cause
Déroulé : L’enseignant montre une animation permettant de découvrir et d’analyser le phénomène de l’illusion de cause, tel que décrit dans les années 1940 par le psychologue Albert Michotte. Les élèves analysent l’animation et les facteurs qui favorisent l’illusion de cause (Phase 1). L’enseignant peut décider de mettre les élèves en situation, en les mettant au défi de modéliser l’illusion et de la faire apparaître et disparaître (phases 2 et 3). Alternativement, il pourra directement inciter les élèves à mettre en relation cette «illusion de cause» avec des exemples de la vie de tous les jours, où on conclue «un peu vite» à une relation de cause à effet entre deux événements successifs (phase 4).
Message à emporter : Nous avons tendance à voir des relations de cause à effet même quand il n’y en a pas, lorsque des événements se produisent l’un à la suite de l’autre. L’ordre des évènements nous pousse aussi à croire que le premier est la cause et le second l’effet. Cependant, ça peut être une illusion!
Cette ressource est issue du projet thématique Esprit scientifique, Esprit critique.
Tous droits réservés ©Le Pommier